Sphere packings of dimension 2

Introduction

Sphere packings in two dimensions (2d), i.e., circle packings, are well studied, due to their usage in coherent modulation. The two dimensions represent the in-phase and quadrature (I/Q) components.

The best known 2d packings are subsets of the hexagonal lattice (honeycomb) [Gilbert52, p. 520], [Simon73], [Foschini74]. It was shown in [Foschini74] that a circular subset of the hexagonal lattice is optimal at asymptotically high M, and it was conjectured in [Graham90] that for M ≠ 4, every optimal 2d packing is a subset of the hexagonal lattice, possibly translated. All best known 2d packings comply with this conjecture. Even for M = 4, a translated subset of the hexagonal lattice is optimal, but in this case, there exist also other optimal packings.

Numerical algorithms to design sphere packings were given in [Foschini74], [Graham90]. The best found normalized second moments were tabulated in [Graham90] for all sizes M ≤ 100 and selected larger sizes. The packings were reproduced using an improved algorithm in [Chow95], where it was proven that the algorithm finds the optimal subset of the hexagonal lattice. Hence, if the conjecture in [Graham90] is true, these are optimal packings. Packings designed using the algorithm of [Chow95] are named c2_*.txt in this database.

The database also contains many suboptimal packings which have been studied in the past. Such packings include quadrature amplitude modulation (QAM) and phase shift keying (PSK) constellations, which form the most popular modulation formats in coherent digital communications, and various special packings from other sources.

The most power-efficient 2d packing, in the sense of maximizing γ, is the equilateral triangle (M = 3). It is the only 2d packing with a positive γ. The highest gain for any 2d packing in the database is G = 0.815 dB and occurs for M = 253, but it would not be hard to design a constellation with marginally higher gains by intersecting the hexagonal lattice with an even large circle. As M → ∞, the gain asymptotically tends to G → 10log₁₀(2π/(3√3)) = 0.825 dB, which equals the gain of the hexagonal lattice over the cubic lattice [Calderbank87, Sec. IV], [Conway99, pp. 7, 73–74, 110].

The 2d packings in the database are, in most cases, rotated and scaled so that the first coordinate is an integer and the second coordinate is a rational number times √3.

Database

File	N	M	d	E	En	κ	Lat	β	Eb	CFM [dB]	γ [dB]	G [dB]	Comment
BPSK2_2	2	2	2	1	0.25	1	Y	1	1	6.0206	0	-1.76091
PSK2_3	2	3	1.73205	1	0.333333	1	Y	1.58496	0.63093	4.77121	0.750803	0	An equilateral triangle, or a 2d simplex [Gilbert52], [Cahn59], [Pierce80], [Ekanayake82].
tri2_4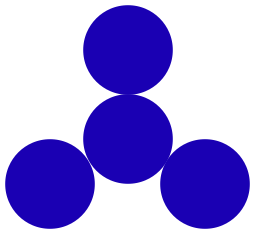	2	4	1	0.75	0.75	1.33333	Y	2	0.375	1.24939	-1.76091	-1.76091	An equilateral triangle with a central point [Thomas74].
QPSK2_4	2	4	1.41421	1	0.5	1	Y	2	0.5	3.0103	0	0	A square. Quadrature phase shift keying (QPSK), possibly the most common coherent modulation format. Used in the Bell 201 modem at 2.4 kbit/s about 1962 and later standardized in V.26 [Forney84], [Hanzo04, Sec. 8.1].
QAM2_4	2	4	2	2	0.5	1	Y	2	1	3.0103	0	0	Another square [Gilbert52], [Campopiano62], equivalent to QPSK2_4 by rotation.
doublesimplex2_4	2	4	2	2	0.5	1.25	Y	2	1	3.0103	0	0	Two equilateral triangles that share an edge. Has the same En as QPSK. Every rhombic packing with a vertex angle between 60° and 120° is equally good [Foschini74], [Forney84], [Graham90]. Described as a Voronoi constellation in [Forney89b].
PSK2_5	2	5	1.17557	1	0.723607	1	N	2.32193	0.430677	1.40497	-0.957139	-0.355939	A pentagon [Karlsson10b].
c2_5	2	5	2	2.72	0.68	1.32526	Y	2.32193	1.17144	1.67491	-0.687201	-0.0860017	[Gilbert52], [Graham90], [Karlsson10b]
PSK2_6	2	6	1	1	1	1	Y	2.58496	0.386853	0	-1.89606	-0.791812	A hexagon.
c2_6	2	6	6	29	0.805556	1.23781	Y	2.58496	11.2187	0.939045	-0.957012	0.147233	[Gilbert52], [Karlsson10b]
PSK2_7	2	7	0.867767	1	1.32799	1	N	2.80735	0.356207	-1.23193	-2.76956	-1.23193	A heptagon.
c2_7	2	7	2	3.42857	0.857143	1.16667	Y	2.80735	1.22128	0.669468	-0.868159	0.669468	A hexagon with a central point [Gilbert52], [Foschini74], [Graham90], [Karlsson10b]. The “kissing” packing, i.e., a central circle surrounded by the maximum number of touching circles [Agrell09].
PSK2_8	2	8	0.765367	1	1.70711	1	N	3	0.333333	-2.32261	-3.57199	-1.65314	An octagon. Used in the Milgo 4400/48 modem at 4.8 kbit/s around 1967 and later standardized in V.27 [Forney84], [Hanzo04, Sec. 8.1].
doubleQPSK2_8	2	8	2	6.82843	1.70711	1.5	N	3	2.27614	-2.32261	-3.57199	-1.65314	[Proakis01, Sec. 5.2.9]. The same performance as PSK.
square2_8	2	8	1	1.5	1.5	1.11111	Y	3	0.5	-1.76091	-3.0103	-1.09144	[Foschini74], [Thomas74], [Proakis01, Sec. 5.2.9]
rectangle2_8	2	8	2	6	1.5	1.44444	Y	3	2	-1.76091	-3.0103	-1.09144	[Calderbank87], [Proakis01, Sec. 5.2.9]
v29modem2_8	2	8	2	5.5	1.375	1.40496	N	3	1.83333	-1.38303	-2.63241	-0.713559	[Campopiano62]. In the 7.2 kbit/s mode of the V.29 modem standard [Hanzo04, Sec. 8.3]. Similar to star2_8.
DSQ2_8	2	8	2.82843	10	1.25	1.32	Y	3	3.33333	-0.9691	-2.21849	-0.299632	Called 8AMPM in [Ungerboeck82]. [Forney88], [Agrell11b] Described as a Voronoi constellation in [Forney89b].
star2_8	2	8	2	4.73205	1.18301	1.33333	N	3	1.57735	-0.729894	-1.97928	-0.0604262	[Foschini74], [Thomas74]. Incorrectly claimed in [Lucky67], [Proakis01, Sec. 5.2.9] to be optimal. Similar to v29modem2_8.
hepta2_8	2	8	0.867767	0.875	1.16199	1.14286	N	3	0.291667	-0.652013	-1.9014	0.0174548	[Foschini74], [Thomas74]
modem2_8	2	8	2	4.5	1.125	1.33333	Y	3	1.5	-0.511525	-1.76091	0.157943	[Gilbert52], [Foschini74], [Thomas74]. Used in a 4.8 kbit/s Hycom modem [Forney84].
c2_8	2	8	2	4.3125	1.07813	1.33522	Y	3	1.4375	-0.326691	-1.57608	0.342777	[Foschini74], [Forney88]
QAM2_9	2	9	1	1.33333	1.33333	1.25	Y	3.16993	0.42062	-1.24939	-2.2595	0	[Gilbert52]
c2_9	2	9	6	44	1.22222	1.31405	Y	3.16993	13.8805	-0.871502	-1.88161	0.377886
c2_10	2	10	2	5.4	1.35	1.2963	Y	3.32193	1.62556	-1.30334	-2.11004	0.457575	[Gilbert52]
c2_11	2	11	22	724	1.49587	1.30384	Y	3.45943	209.283	-1.74893	-2.37948	0.469555
c2_12	2	12	2	6.33333	1.58333	1.27424	Y	3.58496	1.76664	-1.99572	-2.47148	0.636691
c2_13	2	13	26	1196	1.76923	1.32514	Y	3.70044	323.205	-2.47784	-2.81591	0.532455
c2_14	2	14	2	7.57143	1.89286	1.31328	Y	3.80735	1.98863	-2.77118	-2.98554	0.586743
c2_15	2	15	30	1856	2.06222	1.33329	Y	3.90689	475.058	-3.14335	-3.24564	0.536413
PSK2_16	2	16	0.390181	1	6.56854	1	N	4	0.25	-8.17469	-8.17469	-4.19529	[Simon73]
multiPSK2_16	2	16	2	14.0547	3.51367	1.26435	N	4	3.51367	-5.45761	-5.45761	-1.47821	[Salz71]
v29modem2_16	2	16	2	13.5	3.375	1.41838	N	4	3.375	-5.28274	-5.28274	-1.30334	In the V.29 9.6 kbit/s modem standard [Hanzo04, Sec. 8.3]. It is more tolerant to phase errors than most of the other 16-point packings.
honeycomb2_16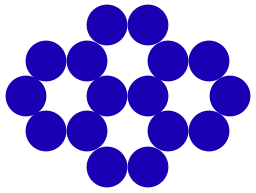	2	16	4	52	3.25	1.31953	Y	4	13	-5.11883	-5.11883	-1.13943	[Thomas74]. Contains holes where further circles would fit.
octa2_16	2	16	2	12.01	3.00249	1.18614	N	4	3.00249	-4.77482	-4.77482	-0.795418	Two octagons forming a star shape [Simon73]. Incorrectly claimed in [Lucky67] to be optimal. Weaker versions of this packing are shown in [Foschini74], [Thomas74], where the ratio between the two radii is higher.
dodeca2_16	2	16	2	11.6962	2.92404	1.22908	N	4	2.92404	-4.65983	-4.65983	-0.68043	Two polygons with the same center [Thomas74].
ennea2_16	2	16	2	10.323	2.58075	1.23538	N	4	2.58075	-4.11746	-4.11746	-0.138062	Two polygons with the same center. Adapted from a packing in [Thomas74] by optimizing the two radii.
penta2_16	2	16	1	2.57377	2.57377	1.28223	N	4	0.643443	-4.1057	-4.1057	-0.126299	[Simon73], [Foschini74]. A suboptimal version, where the ratio between the two nonzero radii is higher, is shown in [Thomas74].
QAM2_16	2	16	2	10	2.5	1.32	Y	4	2.5	-3.9794	-3.9794	0	[Campopiano62], [Simon73], [Foschini74], [Thomas74]. Used in the Codex 9600C modem at 9.6 kbit/s in 1971 [Forney84]. Later used in V.29 [Forney84], V.32 [Hanzo04, Sec. 8.4], and many other standards.
cross2_16	2	16	2	10	2.5	1.31	Y	4	2.5	-3.9794	-3.9794	0	[Forney84]. The same performance as QAM.
t2_16	2	16	2	10	2.5	1.24	Y	4	2.5	-3.9794	-3.9794	0	[Thomas74]. The same performance as QAM.
tri2_16	2	16	2	9.08333	2.27083	1.37497	Y	4	2.27083	-3.56185	-3.56185	0.417547	This packing, suggested in [Simon73], does not have zero mean and can be improved by translation.
hex2_16	2	16	1	2.25	2.25	1.33333	Y	4	0.5625	-3.52183	-3.52183	0.457575	Incorrectly claimed in [Simon73] to be optimal.
compact2_16	2	16	2	8.82813	2.20703	1.33249	Y	4	2.20703	-3.43808	-3.43808	0.541315	[Conway83]. The same constellation as tri2_16, but recentered to zero mean.
c2_16	2	16	4	35	2.1875	1.31673	Y	4	8.75	-3.39948	-3.39948	0.579919	Conjectured optimal in [Conway83], where it was described as a Voronoi code. A similar constellation, optimized for a slightly different criterion, was shown in [Foschini74]. Also shown in [Forney88], [Forney89b], [Graham90].
c2_17	2	17	2	9.24567	2.31142	1.30943	Y	4.08746	2.26196	-3.63879	-3.54485	0.620901
c2_18	2	18	18	788	2.4321	1.30091	Y	4.16993	188.972	-3.85981	-3.67913	0.663165
c2_19	2	19	2	10.1053	2.52632	1.28646	Y	4.24793	2.37887	-4.02488	-3.76371	0.746336	[Simon73], [Foschini74], [Graham90], [Karlsson10b]
c2_20	2	20	8	174.88	2.7325	1.33446	Y	4.32193	40.4634	-4.3656	-4.02943	0.640422
c2_21	2	21	2	11.5646	2.89116	1.33614	Y	4.39232	2.63292	-4.61072	-4.20438	0.618071
greedy2_22	2	22	22	1466	3.02893	1.3312	Y	4.45943	328.741	-4.81289	-4.34069	0.627794	The smallest size for which the “greedy algorithm” does not yield the best known packing [Graham90].
c2_22	2	22	2	12.0909	3.02273	1.32517	Y	4.45943	2.71131	-4.80399	-4.33179	0.636691	[Graham90]
c2_23	2	23	46	6668	3.15123	1.32359	Y	4.52356	1474.06	-4.9848	-4.45059	0.657915
c2_24	2	24	24	1895	3.28993	1.32438	Y	4.58496	413.308	-5.17187	-4.57911	0.663899
c2_25	2	25	2	13.6768	3.4192	1.3216	Y	4.64386	2.94514	-5.33925	-4.69106	0.681355
c2_26	2	26	26	2403	3.55473	1.3212	Y	4.70044	511.229	-5.50807	-4.80729	0.689817
c2_27	2	27	2	14.6667	3.66667	1.31405	Y	4.75489	3.08455	-5.64271	-4.89191	0.725507
c2_28	2	28	2	15.2908	3.8227	1.32283	Y	4.80735	3.18071	-5.82371	-5.02524	0.708418
c2_29	2	29	2	15.9144	3.9786	1.33041	Y	4.85798	3.27593	-5.9973	-5.15334	0.692768
c2_30	2	30	2	16.4667	4.11667	1.32939	Y	4.90689	3.35583	-6.14546	-5.25799	0.69701
c2_31	2	31	2	17.0323	4.25806	1.32369	Y	4.9542	3.43795	-6.29212	-5.36299	0.697578	[Karlsson10b]
skewcross2_32	2	32	1	9.57356	9.57356	1.30175	N	5	1.91471	-9.81073	-8.84163	-2.67863	This irregular constellation was optimized for use in a certain trellis-coded modulation scheme [Calderbank87].
multiPSK2_32	2	32	2	36.5072	9.1268	1.48481	N	5	7.30144	-9.60318	-8.63408	-2.47108	[Salz71]
honeycomb2_32	2	32	2	26.5	6.625	1.33001	Y	5	5.3	-8.21186	-7.24276	-1.07975	[Thomas74]. Contains holes where further circles would fit.
tb2_32	2	32	2	21.7763	5.44407	1.25153	N	5	4.35526	-7.35924	-6.39014	-0.227132	[Thomas74]
circb2_32	2	32	1	5.35348	5.35348	1.2956	N	5	1.0707	-7.28636	-6.31726	-0.154258	Adapted from a packing in [Thomas74] by optimizing the radii.
DSQ2_32	2	32	2.82843	42	5.25	1.38095	Y	5	8.4	-7.20159	-6.23249	-0.0694886	Called 32AMPM in [Ungerboeck82] and "square" in [Forney89a]. Described as a Voronoi constellation in [Forney89b].
circa2_32	2	32	1	5.23537	5.23537	1.27447	N	5	1.04707	-7.18947	-6.22037	-0.0573697	Adapted from a packing in [Thomas74] by optimizing the radii.
ta2_32	2	32	2	20.0011	5.00028	1.31309	N	5	4.00023	-6.98994	-6.02084	0.142159	[Thomas74]
cross2_32	2	32	2	20	5	1.31	Y	5	4	-6.9897	-6.0206	0.142404	[Campopiano62], [Thomas74], [Forney84]. In the V.32 9.6 kbit/s modem standard [Hanzo04, Sec. 8.4].
tri2_32	2	32	1	4.6875	4.6875	1.28853	Y	5	0.9375	-6.70941	-5.74031	0.422692	[Thomas74]
cs2_32	2	32	1	4.4375	4.4375	1.34418	Y	5	0.8875	-6.47138	-5.50228	0.660721	This packing, suggested in [Calderbank87], does not have zero mean and can be improved by translation.
c2_32	2	32	32	4503	4.39746	1.32511	Y	5	900.6	-6.43202	-5.46292	0.700085	[Forney84]
c2_33	2	33	2	18.0826	4.52066	1.32237	Y	5.04439	3.5847	-6.55202	-5.54453	0.717968
c2_34	2	34	34	5370	4.64533	1.32016	Y	5.08746	1055.54	-6.67016	-5.62575	0.733462
c2_35	2	35	2	19.1118	4.77796	1.31987	Y	5.12928	3.72602	-6.79242	-5.71246	0.740852
c2_36	2	36	12	707	4.90972	1.31919	Y	5.16993	136.752	-6.91057	-5.79633	0.748599
c2_37	2	37	2	20.1081	5.02703	1.31547	Y	5.20945	3.85993	-7.01311	-5.86579	0.7684
c2_38	2	38	2	20.8089	5.20222	1.32791	Y	5.24793	3.96516	-7.16188	-5.98261	0.738621
c2_39	2	39	26	3624	5.36095	1.33298	Y	5.2854	685.662	-7.29241	-6.08223	0.723909
c2_40	2	40	2	22.0325	5.50812	1.33052	Y	5.32193	4.13995	-7.41004	-6.16995	0.719096
c2_41	2	41	82	37952	5.64426	1.32988	Y	5.35755	7083.83	-7.51607	-6.24701	0.723018
c2_42	2	42	2	23.0476	5.7619	1.3258	Y	5.39232	4.27416	-7.60566	-6.30851	0.740665
c2_43	2	43	86	43696	5.90806	1.32823	Y	5.42626	8052.68	-7.71445	-6.39004	0.736533
c2_44	2	44	2	24.1591	6.03977	1.32735	Y	5.45943	4.4252	-7.81021	-6.45933	0.742966
c2_45	2	45	90	50024	6.1758	1.32738	Y	5.49185	9108.77	-7.90693	-6.53034	0.74608
c2_46	2	46	2	25.2571	6.31427	1.32791	Y	5.52356	4.57261	-8.00323	-6.60164	0.74738
c2_47	2	47	94	57040	6.45541	1.32897	Y	5.55459	10269.	-8.09924	-6.67332	0.746828
c2_48	2	48	2	26.3333	6.58333	1.32719	Y	5.58496	4.71504	-8.18446	-6.73486	0.755008
cb2_48	2	48	6	237	6.58333	1.32735	Y	5.58496	42.4354	-8.18446	-6.73486	0.755008	The best known packing with M = 48 is not unique. This packing has the same En as c2_48, although they are geometrically different [Graham90].
c2_49	2	49	98	64672	6.73386	1.33019	Y	5.61471	11518.3	-8.28264	-6.80997	0.748258
c2_50	2	50	2	27.4832	6.8708	1.33023	Y	5.64386	4.86958	-8.37007	-6.87491	0.750375
c2_51	2	51	102	73040	7.02038	1.3326	Y	5.67243	12876.3	-8.4636	-6.94652	0.744583
c2_52	2	52	2	28.6346	7.15865	1.33251	Y	5.70044	5.02323	-8.54831	-7.00983	0.745876
c2_53	2	53	106	82060	7.30331	1.33082	Y	5.72792	14326.3	-8.6352	-7.07583	0.743323
c2_54	2	54	54	21641	7.42147	1.32724	Y	5.75489	3760.46	-8.7049	-7.12513	0.756348
c2_55	2	55	2	30.1091	7.52727	1.32273	Y	5.78136	5.20796	-8.76638	-7.16668	0.776049	[Karlsson10b]
c2_56	2	56	14	1504	7.67347	1.32488	Y	5.80735	258.982	-8.84992	-7.23073	0.772197
c2_57	2	57	2	31.2392	7.80979	1.32512	Y	5.83289	5.35569	-8.92639	-7.28815	0.773976
c2_58	2	58	58	26732	7.94649	1.32545	Y	5.85798	4563.35	-9.00175	-7.34487	0.775481
c2_59	2	59	2	32.3516	8.08791	1.32657	Y	5.88264	5.4995	-9.07836	-7.40324	0.774407
c2_60	2	60	30	7406	8.22889	1.32752	Y	5.90689	1253.79	-9.15341	-7.46042	0.773596
c2_61	2	61	2	33.4426	8.36066	1.32694	Y	5.93074	5.63886	-9.2224	-7.51192	0.777597
c2_62	2	62	62	32779	8.52732	1.33228	Y	5.9542	5505.19	-9.30812	-7.58049	0.763663
c2_63	2	63	2	34.7181	8.67952	1.33422	Y	5.97728	5.80834	-9.38496	-7.64052	0.757449
honeycomb2_64	2	64	2	53.5	13.375	1.35138	Y	6	8.91667	-11.2629	-9.50203	-1.05104	[Thomas74] Contains holes where further circles would fit.
circa2_64	2	64	2	45.6353	11.4088	1.33321	N	6	7.60588	-10.5724	-8.8115	-0.360516	Adapted from a packing in [Thomas74] by optimizing the radii.
circb2_64	2	64	2	43.216	10.804	1.29607	N	6	7.20266	-10.3358	-8.57493	-0.123951	Adapted from a packing in [Thomas74] by optimizing the radii.
QAM2_64	2	64	2	42	10.5	1.38095	Y	6	7	-10.2119	-8.45098	0	[Campopiano62], [Thomas74]. Used in the Paradyne MP14400 modem at 14.4 kbit/s in 1980 [Forney84].
cross2_64	2	64	2	41	10.25	1.34265	Y	6	6.83333	-10.1072	-8.34633	0.104654	[Forney84], [Forney88]
hex2_64	2	64	2	41	10.25	1.34206	Y	6	6.83333	-10.1072	-8.34633	0.104654	[Calderbank87]
circular2_64	2	64	2	40.9375	10.2344	1.34008	N	6	6.82292	-10.1006	-8.3397	0.11128	Used in the Paradyne 14.4 kbit/s modem [Forney84]. (Called "circular" in [Forney84].)
voronoi2_64	2	64	2	35.4375	8.85938	1.33941	Y	6	5.90625	-9.47403	-7.71312	0.737862	This packing was presented in [Forney89b] as a Voronoi constellation, which enables low-complexity implementation. Combined with translated replicas of itself, it tiles the plane.
tri2_64	2	64	2	36.625	9.15625	1.32363	Y	6	6.10417	-9.61718	-7.85626	0.594717	[Thomas74]
modem2_64	2	64	2	35.4375	8.85938	1.34196	Y	6	5.90625	-9.47403	-7.71312	0.737862	Used in the Codex/ESE SP14.4 modem [Forney84].
c2_64	2	64	2	35.25	8.8125	1.33152	Y	6	5.875	-9.45099	-7.69008	0.760902	[Forney84]
c2_65	2	65	26	6052.48	8.95337	1.33202	Y	6.02237	1005.	-9.51987	-7.74279	0.760421
c2_66	2	66	2	36.3499	9.08747	1.33135	Y	6.04439	6.01381	-9.58443	-7.7915	0.763193
c2_67	2	67	2	36.8572	9.2143	1.32974	Y	6.06609	6.07594	-9.64462	-7.83614	0.769303
c2_68	2	68	34	10802	9.34429	1.32867	Y	6.08746	1774.47	-9.70546	-7.8817	0.773772
c2_69	2	69	2	37.8551	9.46377	1.32652	Y	6.10852	6.19709	-9.76064	-7.92188	0.782936
c2_70	2	70	28	7538.08	9.6149	1.32878	Y	6.12928	1229.85	-9.82945	-7.97595	0.777532
c2_71	2	71	2	39.028	9.75699	1.3295	Y	6.14975	6.34627	-9.89316	-8.02519	0.776308
c2_72	2	72	8	633.667	9.90104	1.33052	Y	6.16993	102.702	-9.95681	-8.07461	0.774262
c2_73	2	73	146	214020	10.0403	1.3307	Y	6.18982	34576.1	-10.0175	-8.1213	0.774326
c2_74	2	74	74	55747	10.1802	1.33096	Y	6.20945	8977.76	-10.0776	-8.16765	0.774135
c2_75	2	75	50	25782.7	10.3131	1.33041	Y	6.22882	4139.25	-10.1339	-8.21042	0.776926
c2_76	2	76	2	41.7895	10.4474	1.33014	Y	6.24793	6.68853	-10.1901	-8.25331	0.779031
c2_77	2	77	154	251468	10.6033	1.33266	Y	6.26679	40127.1	-10.2544	-8.30456	0.772211
c2_78	2	78	26	7266.33	10.749	1.33356	Y	6.2854	1156.06	-10.3137	-8.35096	0.769709
c2_79	2	79	158	271728	10.8848	1.33232	Y	6.30378	43105.6	-10.3682	-8.39279	0.771231
c2_80	2	80	20	4406.81	11.017	1.33162	Y	6.32193	697.068	-10.4206	-8.43275	0.774113
cs2_81	2	81	2	51.4815	12.8704	1.33098	Y	6.33985	8.1203	-11.0959	-9.09572	0.153477	This packing, suggested in [Calderbank87], does not have zero mean and can be improved by translation.
c2_81	2	81	2	44.5926	11.1481	1.33081	Y	6.33985	7.0337	-10.472	-8.47184	0.77736
c2_82	2	82	82	75858	11.2817	1.33023	Y	6.35755	11932.	-10.5237	-8.51144	0.779601
c2_83	2	83	166	314412	11.4099	1.32911	Y	6.37504	49319.2	-10.5728	-8.5486	0.783797
c2_84	2	84	28	9041.67	11.5327	1.32751	Y	6.39232	1414.46	-10.6193	-8.58334	0.789944
c2_85	2	85	2	46.5882	11.6471	1.32534	Y	6.40939	7.26875	-10.6622	-8.61459	0.799118
c2_86	2	86	86	87265	11.7989	1.32736	Y	6.42626	13579.4	-10.7184	-8.65945	0.794245
c2_87	2	87	2	47.7765	11.9441	1.3284	Y	6.44294	7.41532	-10.7715	-8.7013	0.791933
c2_88	2	88	44	23405	12.0894	1.32943	Y	6.45943	3623.38	-10.824	-8.74269	0.789647
c2_89	2	89	2	48.9509	12.2377	1.33084	Y	6.47573	7.55913	-10.877	-8.78472	0.786308
c2_90	2	90	18	4013	12.3858	1.33216	Y	6.49185	618.159	-10.9292	-8.82615	0.783146
c2_91	2	91	2	50.1099	12.5275	1.33265	Y	6.50779	7.69998	-10.9786	-8.8649	0.782278
c2_92	2	92	92	107259	12.6724	1.33251	Y	6.52356	16441.8	-11.0286	-8.90433	0.780321
c2_93	2	93	62	49234.7	12.8082	1.33218	Y	6.53916	7529.2	-11.0749	-8.94026	0.78149
c2_94	2	94	94	114345	12.9408	1.33162	Y	6.55459	17445.	-11.1196	-8.97476	0.783702
c2_95	2	95	38	18893.3	13.084	1.33213	Y	6.56986	2875.75	-11.1674	-9.01244	0.782364
c2_96	2	96	2	52.875	13.2188	1.33184	Y	6.58496	8.02966	-11.2119	-9.04697	0.78382
c2_97	2	97	194	502760	13.3585	1.33205	Y	6.59991	76176.8	-11.2576	-9.08279	0.783627
c2_98	2	98	14	2644.73	13.4935	1.3317	Y	6.61471	399.826	-11.3013	-9.11675	0.784944
c2_99	2	99	22	6594.96	13.626	1.3312	Y	6.62936	994.812	-11.3437	-9.14956	0.787078
c2_100	2	100	2	55.0148	13.7537	1.33028	Y	6.64386	8.28055	-11.3842	-9.18059	0.790644
c2_101	2	101	202	566572	13.8852	1.32975	Y	6.65821	85093.7	-11.4255	-9.21255	0.792964
c2_102	2	102	2	56.0392	14.0098	1.32869	Y	6.67243	8.39863	-11.4643	-9.24208	0.797381
c2_103	2	103	206	601124	14.1654	1.33064	Y	6.6865	89901.1	-11.5123	-9.28091	0.792193
c2_104	2	104	2	57.2504	14.3126	1.33154	Y	6.70044	8.54427	-11.5572	-9.31675	0.789677
c2_105	2	105	14	2832.85	14.4533	1.33178	Y	6.71425	421.917	-11.5997	-9.35031	0.789141
c2_106	2	106	2	58.3578	14.5894	1.33162	Y	6.72792	8.67397	-11.6404	-9.38218	0.789993
c2_107	2	107	214	674724	14.7333	1.3322	Y	6.74147	100086.	-11.683	-9.41604	0.78856
c2_108	2	108	2	59.4815	14.8704	1.33213	Y	6.75489	8.8057	-11.7232	-9.44764	0.789107
c2_109	2	109	218	713284	15.0089	1.33221	Y	6.76818	105388.	-11.7635	-9.47937	0.78923
c2_110	2	110	2	60.6	15.15	1.33256	Y	6.78136	8.93626	-11.8041	-9.51156	0.788626
c2_111	2	111	222	753728	15.2936	1.33289	Y	6.79442	110933.	-11.8451	-9.54417	0.787327
c2_112	2	112	16	3950.45	15.4314	1.3328	Y	6.80735	580.321	-11.8841	-9.57488	0.787652
c2_113	2	113	2	62.258	15.5645	1.332	Y	6.82018	9.12849	-11.9213	-9.60399	0.789318
c2_114	2	114	114	203975	15.6952	1.33149	Y	6.83289	29851.9	-11.9577	-9.63223	0.7916
c2_115	2	115	230	837104	15.8243	1.33086	Y	6.84549	122285.	-11.9932	-9.65979	0.794299
c2_116	2	116	8	1021.42	15.9596	1.33071	Y	6.85798	148.938	-12.0302	-9.68887	0.795233
c2_117	2	117	2	64.3726	16.0931	1.33042	Y	6.87036	9.3696	-12.0664	-9.71721	0.796659
c2_118	2	118	118	225977	16.2293	1.33032	Y	6.88264	32832.9	-12.103	-9.74605	0.797344
c2_119	2	119	238	926764	16.3612	1.32988	Y	6.89482	134415.	-12.1382	-9.77352	0.799155
c2_120	2	120	60	59362.3	16.4895	1.3292	Y	6.90689	8594.64	-12.1721	-9.79985	0.801879
c2_121	2	121	2	66.4463	16.6116	1.32815	Y	6.91886	9.60364	-12.2041	-9.82436	0.806193
c2_122	2	122	122	249576	16.7681	1.32992	Y	6.93074	36010.	-12.2448	-9.85764	0.80151
c2_123	2	123	2	67.6788	16.9197	1.33113	Y	6.94251	9.74845	-12.2839	-9.88936	0.798162
c2_124	2	124	62	65621.3	17.0711	1.3322	Y	6.9542	9436.21	-12.3226	-9.92074	0.794927
c2_125	2	125	2	68.8622	17.2156	1.33263	Y	6.96578	9.88578	-12.3592	-9.95011	0.793495
c2_126	2	126	126	275618	17.3607	1.33313	Y	6.97728	39502.2	-12.3957	-9.9794	0.791923
c2_127	2	127	254	1129132	17.5016	1.33328	Y	6.98868	161566.	-12.4308	-10.0074	0.79142
fivecircle2_128	2	128	2	115.539	28.8846	1.33698	N	7	16.5055	-14.6067	-12.1763	-1.35014	Adapted from a packing in [Thomas74] by optimizing the radii.
sixcircle2_128	2	128	2	85.7217	21.4304	1.32041	N	7	12.246	-13.3103	-10.8799	-0.0537841	Adapted from a packing in [Thomas74] by optimizing the radii.
DSQ2_128	2	128	2.82843	170	21.25	1.39529	Y	7	24.2857	-13.2736	-10.8432	-0.0170646	128-ary double square (DSQ) packing is used in the 10-gigabit Ethernet standard 10GBASE-T.
cross2_128	2	128	2	82	20.5	1.34265	Y	7	11.7143	-13.1175	-10.6872	0.138986	[Forney84], [Calderbank87]. In the V.33 14.4 kbit/s modem standard [Hanzo04, Sec. 8.5].
b2_128	2	128	2	82	20.5	1.34265	Y	7	11.7143	-13.1175	-10.6872	0.138986	[Campopiano62], [Thomas74]. Has, as pointed out in [Forney84], the same performance as cross2_128, although the constellations are not equivalent.
tri2_128	2	128	2	71.962	17.9905	1.32928	N	7	10.2803	-12.5504	-10.1201	0.706091	[Thomas74]
c2_128	2	128	2	70.5442	17.636	1.33265	Y	7	10.0777	-12.464	-10.0336	0.792512
c2_129	2	129	258	1182920	17.7712	1.33247	Y	7.01123	168718.	-12.4972	-10.0598	0.793428
c2_130	2	130	2	71.6154	17.9038	1.33212	Y	7.02237	10.1982	-12.5295	-10.0852	0.794921
c2_131	2	131	262	1238720	18.0456	1.33245	Y	7.03342	176119.	-12.5637	-10.1126	0.794215
c2_132	2	132	22	8799.67	18.1811	1.33232	Y	7.04439	1249.17	-12.5962	-10.1384	0.794992
c2_133	2	133	266	1296160	18.3187	1.33232	Y	7.05528	183715.	-12.629	-10.1644	0.795273
c2_134	2	134	134	331356	18.4538	1.3321	Y	7.06609	46893.8	-12.6609	-10.1897	0.796151
c2_135	2	135	2	74.348	18.587	1.33181	Y	7.07682	10.5059	-12.6921	-10.2143	0.797443
c2_136	2	136	68	86588.3	18.7258	1.33192	Y	7.08746	12217.1	-12.7244	-10.2401	0.797414
c2_137	2	137	274	1416196	18.8635	1.33191	Y	7.09803	199520.	-12.7562	-10.2654	0.797654
c2_138	2	138	138	361829	18.9996	1.33182	Y	7.10852	50900.7	-12.7875	-10.2903	0.798241
c2_139	2	139	2	76.5288	19.1322	1.33148	Y	7.11894	10.75	-12.8176	-10.3141	0.799632
c2_140	2	140	70	94409	19.2671	1.33132	Y	7.12928	13242.4	-12.8482	-10.3383	0.800462
c2_141	2	141	2	77.5887	19.3972	1.33086	Y	7.13955	10.8674	-12.8774	-10.3613	0.802386
c2_142	2	142	2	78.1704	19.5426	1.33145	Y	7.14975	10.9333	-12.9098	-10.3875	0.800855
c2_143	2	143	2	78.752	19.688	1.33203	Y	7.15987	10.9991	-12.942	-10.4136	0.799354
c2_144	2	144	2	79.3189	19.8297	1.33228	Y	7.16993	11.0627	-12.9732	-10.4386	0.798683
c2_145	2	145	290	1679736	19.9731	1.33266	Y	7.17991	233949.	-13.0045	-10.4639	0.797662
c2_146	2	146	2	80.4519	20.113	1.3328	Y	7.18982	11.1897	-13.0348	-10.4882	0.797406
c2_147	2	147	294	1751000	20.2578	1.33328	Y	7.19967	243206.	-13.0659	-10.5134	0.796101
c2_148	2	148	74	111691.	20.3965	1.33323	Y	7.20945	15492.3	-13.0956	-10.5371	0.796104
c2_149	2	149	2	82.1212	20.5303	1.33253	Y	7.21917	11.3754	-13.124	-10.5597	0.797154
c2_150	2	150	50	51645.7	20.6583	1.33191	Y	7.22882	7144.41	-13.1509	-10.5809	0.799411
c2_151	2	151	2	83.1258	20.7815	1.33107	Y	7.2384	11.484	-13.1768	-10.6009	0.80264
c2_152	2	152	38	30216.8	20.9258	1.33154	Y	7.24793	4169.03	-13.2068	-10.6253	0.801442
c2_153	2	153	306	1972412	21.0647	1.33164	Y	7.25739	271780.	-13.2355	-10.6483	0.801376
c2_154	2	154	154	502802	21.201	1.33158	Y	7.26679	69191.8	-13.2636	-10.6707	0.801846
c2_155	2	155	2	85.3349	21.3337	1.33132	Y	7.27612	11.7281	-13.2907	-10.6923	0.803026
c2_156	2	156	24	12366.4	21.4694	1.33124	Y	7.2854	1697.42	-13.3182	-10.7143	0.803608
c2_157	2	157	314	2129984	21.6031	1.33105	Y	7.29462	291994.	-13.3452	-10.7357	0.804563
c2_158	2	158	158	542773	21.7422	1.33118	Y	7.30378	74314.	-13.373	-10.7582	0.804443
c2_159	2	159	2	87.5173	21.8793	1.33118	Y	7.31288	11.9675	-13.4003	-10.7801	0.804721
c2_160	2	160	40	35230.3	22.0189	1.33133	Y	7.32193	4811.61	-13.428	-10.8023	0.804501
c2_161	2	161	322	2297116	22.155	1.33126	Y	7.33092	313346.	-13.4547	-10.8237	0.804975
c2_162	2	162	162	584939	22.2885	1.33104	Y	7.33985	79693.6	-13.4808	-10.8445	0.805941
c2_163	2	163	2	89.6687	22.4172	1.33057	Y	7.34873	12.2019	-13.5058	-10.8643	0.807828
c2_164	2	164	2	90.2855	22.5714	1.33167	Y	7.35755	12.2711	-13.5356	-10.8888	0.804781
c2_165	2	165	110	274936	22.722	1.33247	Y	7.36632	37323.4	-13.5645	-10.9126	0.802464
c2_166	2	166	166	630273	22.8724	1.33321	Y	7.37504	85460.3	-13.5931	-10.9361	0.800202
c2_167	2	167	334	2567836	23.0184	1.33363	Y	7.3837	347771.	-13.6207	-10.9586	0.798825
c2_168	2	168	2	92.6186	23.1547	1.33316	Y	7.39232	12.529	-13.6464	-10.9792	0.799269
c2_169	2	169	338	2660756	23.2901	1.33299	Y	7.40088	359519.	-13.6717	-10.9995	0.799864
c2_170	2	170	2	93.6854	23.4213	1.3326	Y	7.40939	12.6441	-13.6961	-11.0189	0.801235
c2_171	2	171	342	2755160	23.5556	1.33242	Y	7.41785	371423.	-13.7209	-11.0388	0.802031
c2_172	2	172	2	94.7514	23.6878	1.33213	Y	7.42626	12.759	-13.7453	-11.0581	0.803194
c2_173	2	173	346	2852008	23.8231	1.332	Y	7.43463	383611.	-13.77	-11.078	0.803787
c2_174	2	174	2	95.8161	23.954	1.33166	Y	7.44294	12.8734	-13.7938	-11.0969	0.805164
c2_175	2	175	50	60243.6	24.0974	1.33201	Y	7.45121	8085.07	-13.8197	-11.118	0.804271
c2_176	2	176	2	96.9489	24.2372	1.33214	Y	7.45943	12.9968	-13.8448	-11.1384	0.804041
c2_177	2	177	354	3054944	24.3779	1.33232	Y	7.46761	409093.	-13.87	-11.1588	0.803647
c2_178	2	178	178	776765	24.516	1.33234	Y	7.47573	103905.	-13.8945	-11.1786	0.803724
c2_179	2	179	358	3159556	24.6524	1.33228	Y	7.48382	422185.	-13.9186	-11.198	0.804087
c2_180	2	180	2	99.1611	24.7903	1.33231	Y	7.49185	13.2359	-13.9428	-11.2175	0.804204
c2_181	2	181	362	3267164	24.9318	1.33249	Y	7.49985	435631.	-13.9675	-11.2376	0.803675
c2_182	2	182	26	16945.9	25.068	1.33243	Y	7.50779	2257.11	-13.9912	-11.2567	0.804084
c2_183	2	183	366	3376568	25.2065	1.33249	Y	7.5157	449269.	-14.0151	-11.276	0.804068
c2_184	2	184	2	101.369	25.3422	1.33239	Y	7.52356	13.4735	-14.0384	-11.2948	0.804563
c2_185	2	185	370	3488344	25.481	1.33245	Y	7.53138	463175.	-14.0622	-11.314	0.804507
c2_186	2	186	2	102.462	25.6156	1.3323	Y	7.53916	13.5907	-14.085	-11.3324	0.805161
c2_187	2	187	374	3603092	25.7592	1.33263	Y	7.54689	477427.	-14.1093	-11.3522	0.804295
c2_188	2	188	2	103.6	25.9001	1.3328	Y	7.55459	13.7136	-14.133	-11.3715	0.80389
c2_189	2	189	378	3721112	26.0429	1.33306	Y	7.56224	492065.	-14.1569	-11.391	0.803175
c2_190	2	190	2	104.721	26.1802	1.33303	Y	7.56986	13.8339	-14.1797	-11.4095	0.803377
c2_191	2	191	382	3840928	26.3214	1.33322	Y	7.57743	506891.	-14.2031	-11.4285	0.802929
c2_192	2	192	2	105.833	26.4583	1.33317	Y	7.58496	13.953	-14.2256	-11.4467	0.803196
c2_193	2	193	386	3961856	26.5904	1.33257	Y	7.59246	521815.	-14.2472	-11.464	0.804259
c2_194	2	194	194	1005748	26.723	1.33233	Y	7.59991	132337.	-14.2689	-11.4814	0.805203
c2_195	2	195	2	107.425	26.8563	1.33212	Y	7.60733	14.1213	-14.2905	-11.4987	0.806038
c2_196	2	196	14	5290.02	26.9899	1.33192	Y	7.61471	694.711	-14.312	-11.5161	0.806821
c2_197	2	197	394	4210288	27.1219	1.33165	Y	7.62205	552382.	-14.3332	-11.5331	0.807855
c2_198	2	198	198	1068356	27.2512	1.33127	Y	7.62936	140032.	-14.3539	-11.5496	0.809294
c2_199	2	199	2	109.508	27.3769	1.33075	Y	7.63662	14.3398	-14.3738	-11.5654	0.811299
c2_200	2	200	80	176151.	27.5236	1.33124	Y	7.64386	23044.8	-14.397	-11.5845	0.80997
c2_201	2	201	134	496772	27.6661	1.3315	Y	7.65105	64928.6	-14.4195	-11.6029	0.809312
c2_202	2	202	202	1134621	27.8066	1.33165	Y	7.65821	148157.	-14.4415	-11.6208	0.808967
c2_203	2	203	2	111.777	27.9442	1.33166	Y	7.66534	14.5821	-14.4629	-11.6382	0.809083
c2_204	2	204	68	129862.	28.0843	1.3318	Y	7.67243	16925.8	-14.4846	-11.6559	0.808816
c2_205	2	205	82	189768	28.2225	1.33184	Y	7.67948	24711.	-14.506	-11.6732	0.808836
c2_206	2	206	206	1203705	28.3652	1.33211	Y	7.6865	156600.	-14.5279	-11.6912	0.80817
c2_207	2	207	2	114.024	28.506	1.33227	Y	7.69349	14.8208	-14.5494	-11.7087	0.807799
c2_208	2	208	32	29336.6	28.649	1.33255	Y	7.70044	3809.73	-14.5711	-11.7265	0.807094
c2_209	2	209	418	5030148	28.7891	1.33267	Y	7.70736	652642.	-14.5923	-11.7438	0.806839
c2_210	2	210	28	22679.	28.9273	1.3327	Y	7.71425	2939.88	-14.6131	-11.7607	0.806875
c2_211	2	211	2	116.246	29.0616	1.33255	Y	7.7211	15.0557	-14.6332	-11.777	0.807484
c2_212	2	212	212	1312855	29.2109	1.33311	Y	7.72792	169885.	-14.6555	-11.7954	0.805862
c2_213	2	213	142	591853.	29.352	1.333	Y	7.73471	76519.1	-14.6764	-11.8125	0.805472
c2_214	2	214	214	1350436	29.4881	1.33293	Y	7.74147	174442.	-14.6965	-11.8288	0.805819
c2_215	2	215	430	5478144	29.6276	1.33302	Y	7.74819	707022.	-14.717	-11.8456	0.80566
c2_216	2	216	108	347207	29.7674	1.33312	Y	7.75489	44772.7	-14.7374	-11.8623	0.805462
c2_217	2	217	62	114953.	29.9044	1.33304	Y	7.76155	14810.5	-14.7574	-11.8785	0.805669
c2_218	2	218	218	1427503	30.0375	1.33282	Y	7.76818	183763.	-14.7766	-11.894	0.806444
c2_219	2	219	2	120.676	30.1689	1.3325	Y	7.77479	15.5214	-14.7956	-11.9093	0.807451
c2_220	2	220	88	234680.	30.3048	1.33245	Y	7.78136	30159.3	-14.8151	-11.9252	0.807812
c2_221	2	221	2	121.749	30.4373	1.33223	Y	7.7879	15.6331	-14.8341	-11.9405	0.808651
c2_222	2	222	74	167412.	30.572	1.33211	Y	7.79442	21478.5	-14.8532	-11.956	0.80917
c2_223	2	223	2	122.822	30.7055	1.33195	Y	7.8009	15.7446	-14.8722	-11.9713	0.809858
c2_224	2	224	112	386870.	30.8411	1.33187	Y	7.80735	49552.	-14.8913	-11.9869	0.810243
c2_225	2	225	2	123.893	30.9733	1.33166	Y	7.81378	15.8557	-14.9099	-12.0019	0.811088
c2_226	2	226	226	1589469	31.1197	1.33207	Y	7.82018	203252.	-14.9304	-12.0188	0.809961
c2_227	2	227	2	125.053	31.2632	1.33233	Y	7.82655	15.978	-14.9503	-12.0352	0.809236
c2_228	2	228	2	125.628	31.4069	1.33259	Y	7.83289	16.0385	-14.9703	-12.0516	0.808493
c2_229	2	229	458	6617624	31.5479	1.33267	Y	7.8392	844170.	-14.9897	-12.0676	0.808125
c2_230	2	230	2	126.722	31.6804	1.33246	Y	7.84549	16.1522	-15.0079	-12.0823	0.808931
c2_231	2	231	462	6792296	31.8224	1.33265	Y	7.85175	865068.	-15.0273	-12.0983	0.808439
c2_232	2	232	58	107516	31.9608	1.33268	Y	7.85798	13682.4	-15.0462	-12.1137	0.808436
c2_233	2	233	466	6970520	32.0991	1.33271	Y	7.86419	886363.	-15.0649	-12.129	0.808434
c2_234	2	234	234	1765148	32.2366	1.33271	Y	7.87036	224278.	-15.0835	-12.1441	0.808553
c2_235	2	235	470	7152096	32.3771	1.33282	Y	7.87652	908028.	-15.1024	-12.1596	0.80827
c2_236	2	236	118	452761	32.5166	1.3329	Y	7.88264	57437.7	-15.121	-12.1749	0.808116
c2_237	2	237	474	7337024	32.656	1.33298	Y	7.88874	930062.	-15.1396	-12.1902	0.807975
c2_238	2	238	2	131.168	32.792	1.33291	Y	7.89482	16.6145	-15.1577	-12.2049	0.80829
c2_239	2	239	478	7525600	32.9371	1.33322	Y	7.90087	952503.	-15.1769	-12.2207	0.807404
c2_240	2	240	240	1905251	33.0773	1.33321	Y	7.90689	240961.	-15.1953	-12.2358	0.807169
c2_241	2	241	2	132.846	33.2116	1.33292	Y	7.91289	16.7886	-15.2129	-12.2501	0.8077
c2_242	2	242	22	16140.8	33.3488	1.33301	Y	7.91886	2038.27	-15.2308	-12.2648	0.807858
c2_243	2	243	2	133.94	33.4851	1.33296	Y	7.92481	16.9014	-15.2485	-12.2792	0.808127
c2_244	2	244	122	500380.	33.6187	1.33269	Y	7.93074	63093.8	-15.2658	-12.2933	0.808745
c2_245	2	245	2	135.002	33.7505	1.33248	Y	7.93664	17.01	-15.2828	-12.307	0.809587
c2_246	2	246	246	2050463	33.883	1.3323	Y	7.94251	258163.	-15.2998	-12.3208	0.810331
c2_247	2	247	494	8301032	34.0156	1.33212	Y	7.94837	1044369.	-15.3168	-12.3346	0.811057
c2_248	2	248	62	131273.	34.1502	1.33201	Y	7.9542	16503.7	-15.3339	-12.3486	0.811526
c2_249	2	249	2	137.139	34.2848	1.3319	Y	7.96	17.2285	-15.351	-12.3625	0.811988
c2_250	2	250	250	2151251	34.42	1.33181	Y	7.96578	270061.	-15.3681	-12.3764	0.81237
c2_251	2	251	502	8707672	34.5537	1.33167	Y	7.97154	1092345.	-15.3849	-12.3901	0.812941
c2_252	2	252	126	550666.	34.6855	1.33146	Y	7.97728	69029.3	-15.4015	-12.4035	0.813751
c2_253	2	253	2	139.257	34.8142	1.33116	Y	7.98299	17.4442	-15.4176	-12.4165	0.814925
c2_254	2	254	254	2255701	34.9634	1.33165	Y	7.98868	282362.	-15.4361	-12.432	0.813552
c2_255	2	255	30	31598.4	35.1093	1.33198	Y	7.99435	3952.58	-15.4542	-12.447	0.812605
c2_256	2	256	128	577595	35.2536	1.33224	Y	8	72199.4	-15.472	-12.4617	0.811854
QAM2_256	2	256	2	170	42.5	1.39529	Y	8	21.25	-16.2839	-13.2736	0	[Campopiano62], [Forney84]. In the 12 kbit/s mode of the V.33 modem standard [Hanzo04, Sec. 8.5].
DSQ2_512	2	512	2.82843	682	85.25	1.39883	Y	9	75.7778	-19.3069	-15.7851	-0.00424738
cross2_512	2	512	2	330	82.5	1.35056	Y	9	36.6667	-19.1645	-15.6427	0.138157
QAM2_1024	2	1024	2	682	170.5	1.39883	Y	10	68.2	-22.3172	-18.3378	0